DeepSORT之马氏距离

发表于 | 分类于 | 阅读次数

本次继续研究 DeepSORT 论文中的算法原理。

马氏距离（Mahalanobis Distance）

欧氏距离

首先，解释马氏距离前不得不提一下欧式距离（Euclidean Distance）

  • 欧式距离指的是在 $n$ 维空间中两个点之间的真实距离。取两个 $n$ 维向量 $\mathbb{a}(x_{11}, x_{12}, \dots , x_{1n})$ 和 $\mathbb{b}(x_{21}, x_{22}, \dots, x_{2n})$ 之间的欧式距离：
\[d_{12} = \sqrt{\sum_{i=1}^n{(x_{1i}-x_{2i})^2}}\]
  • 标准化欧式距离（Standardized Euclidean Distance）是因为一个数据的各维分量的分布不一样，因此先将各个分量都“标准化”到均值、方差相等。假设样本集 $X$ 的均值（mean）为 $m$ ，标准差（standard deviation）为 $s$ ， $X$ 的“标准化变量”表示为： $X^* = \frac{X - m}{s}$ 。将数据标准化处理之后，均值变为0，方差变为1，即服从标准正态分布。标准化欧氏距离公式：
\[d_{12} = \sqrt{\sum_{i=1}^n{\left(\frac{x_{1i}-x_{2i}}{s_i}\right)^2}}\]

其中如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)。

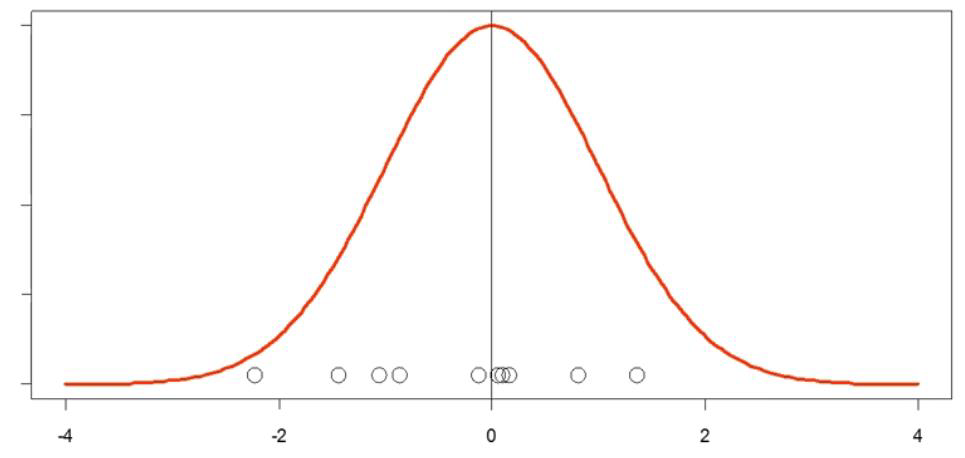
例如下图中，圆点代表每个点，这些点作为变量符合一定的分布。取圆点的某一点： $x_i$ 计算与这些点的均值 $\overline{x}$ 欧氏距离。

\[d = x_i - \overline{x}\]

The distance of a point from the mean in univariate space is a simple measure: $x_i - \overline{x}$

This type of distance is called Euclidean distance

b56540e6a0ea77811928b923c3a55e0a.png

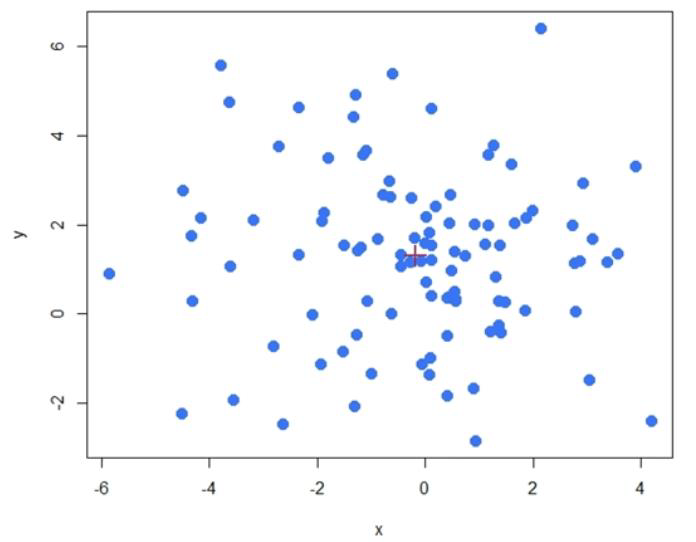
一般我们解决的问题都是在多维情况下，对于多维空间中，计算一个点和均值计算欧式距离，则是需要该点在每个维度的分量与每个维度均值进行计算，公式如下：

\[d = \sqrt{(x_i-\overline{x})^2 + (y_i-\overline{y})^2 + \dots + (n_i - \overline{n})^2}\]

This can easily be extended to multivariate space by using the Euclidean distance of a point from the mean.

bd27caafd6b70f79b22a89506fe064e7.png

欧式距离的局限性

欧式距离可以作为一种相似度算法：欧氏距离越小，相似度越大；欧氏距离越大，相似度越小。

然而欧式距离近就一定相似吗？

例如身高和体重，这两个变量拥有不同的单位标准。如果身高用毫米计算，而体重用千克计算，显然差10毫米的身高和差10千克的体重是完全不同的。在欧式距离中，会算作相同的差距。因为欧式距离计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别。

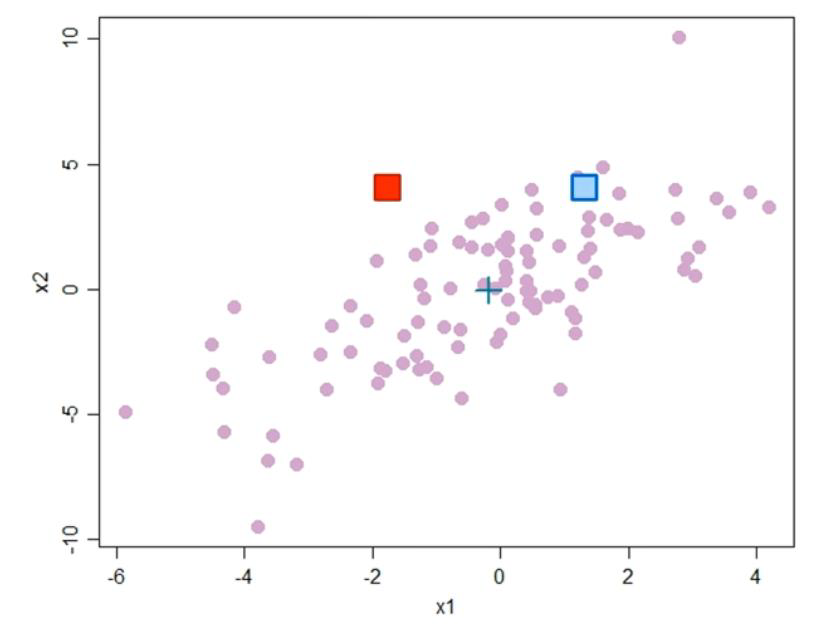
又例如：如图在某个维度具有分布的数据中，这个分布中具有一定程度的协方差。而图中有红色方块和蓝色方块，作为其中的点。如果去计算与均值之间的欧式距离，能看出红色与蓝色和中心点（均值点）距离相同。然而，蓝色方块在一定程度上是位于更为密集的分布中。如何考虑这种有一定分布的两点之间距离，就不能使用欧式距离。

However, Euclidean distance has limitations in real datasets,which often have some degree of covariance.

d741269eb2efba1c6bcebe4cd5070ec3.png

协方差（Covariance）

标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集。面对这样的数据集，当然，可以按照每一维度（feature）独立的计算其方差，但是，通常我们还想了解每个样本中各维度（feature）之间的关系，即度量各个维度之间的之间的相关性，定义协方差为：

\[\mathcal{cov}(X,Y) = \frac{\sum_{i=1}^n{(X_i - \bar{X})(Y_i-\bar{Y})}}{n-1}\]

其中，$X, Y$ 代表两个维度（特征）， $n$ 表示样本的个数。也可写成：

\[\begin{array}{rl} \mathcal{Cov}(X,Y) & = \ E\left[(X - E[X])(Y - E[Y]) \right] \\ & = E[XY] - 2E[Y]E[X] + E[X]E[Y] \\ & = E[XY] - E[X]E[Y] \end{array}\]

当遇到一个样本有多个维度时，可以用 协方差矩阵（Covariance Matrix） 表示：

\[\mathcal{Cov}(X,Y) = \begin{bmatrix} \mathcal{cov}(x_1,x_1) & \mathcal{cov}(x_1,x_2) & \mathcal{cov}(x_1,x_3) \\ \mathcal{cov}(x_2,x_1) & \mathcal{cov}(x_2,x_2) & \mathcal{cov}(x_2,x_3) \\ \mathcal{cov}(x_3,x_1) & \mathcal{cov}(x_3,x_2) & \mathcal{cov}(x_3,x_3) \end{bmatrix}\]

其中根据协方差性质（ $\mathcal{var}$ 表示为方差 ）

\[1. \mathcal{cov}(x,x) = \mathcal{var}(x) \\ \\ 2. \mathcal{cov}(x,y) = \mathcal{cov}(y,x)\]

得到最终协方差矩阵：

\[\mathcal{Cov}(X,Y) = \begin{bmatrix} \mathcal{var}(x_1) & \mathcal{cov}(x_1,x_2) & \mathcal{cov}(x_1,x_3) \\ \mathcal{cov}(x_2,x_1) & \mathcal{var}(x_2) & \mathcal{cov}(x_2,x_3) \\ \mathcal{cov}(x_3,x_1) & \mathcal{cov}(x_3,x_2) & \mathcal{var}(x_3) \end{bmatrix}\]

协方差意义 ：如果结果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，结果为负值就说明负相关的，如果为0，也是就是统计上说的“相互独立”。

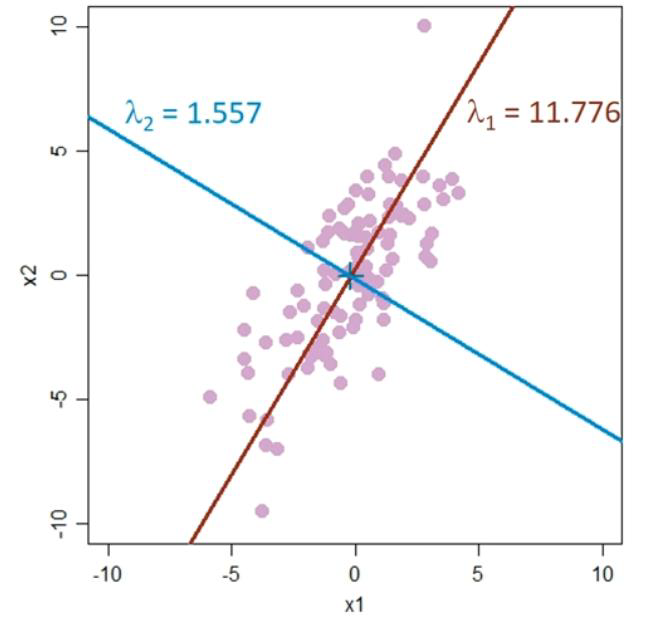
Rescaling to Remove Covariance

\[Ax = \lambda{x}\]

根据上式，可以得到两个特征值 $\lambda_1$ 和 $\lambda_2$ ，根据这两个值垂直关系（因为协方差矩阵是一个实对称矩阵）得到关于中心点的一个坐标轴。将该轴缩小 $\sqrt{\lambda_i}$ 倍，就可根据变换后的尺度上计算两点的距离。这个距离就是马氏距离。

98f847a3174036f06677a06bdf5af523.png

马氏距离

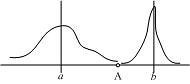
1cdbb0c82e17e01a03cf4f35c712e7cb.png

上图有两个正态分布的总体，它们的均值分别为a和b，但方差不一样，则图中的A点离哪个总体更近？或者说A有更大的概率属于谁？显然，A离左边的更近，A属于左边总体的概率更大，尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。

Mahalanobis distance measure does the following:

  • it transforms the variables into uncorrelated variables
  • and makes their variances equal to 1
  • then calculates simple Euclidean distance.

与欧氏距离不同的是，它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的），并且是尺度无关的(scaleinvariant)，即独立于测量尺度。

  • 若有 $N$ 个样本向量 $X_1 \sim X_N$ ，协方差矩阵记为 $S$ ，均值记为向量 $\mu$ ，其中样本向量 $X$ 到 $\mu$ 的马氏距离表示为：
\[d(X) = \sqrt{(X - \mu)^TS^{-1}(X - \mu)}\]
  • 向量 $X_i$ 与 $X_j$ 之间的马氏距离定义为：
\[d(X_i, X_j) = \sqrt{(X_i - X_j)^TS^{-1}(X_i - X_j)}\]
  • 若协方差矩阵是单位矩阵（各个样本向量之间独立同分布），则 $X_i$ 与 $X_j$ 之间的马氏距离等于他们的欧氏距离：
\[d(X_i, X_j) = \sqrt{(X_i - X_j)^T(X_i - X_j)}\]
  • 若协方差矩阵是对角矩阵，则就是标准化欧氏距离。
  • 欧氏距离&马氏距离

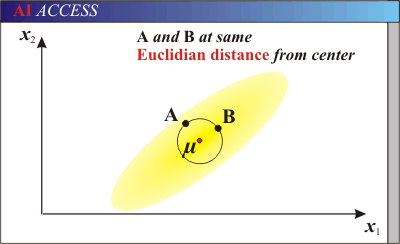
de81c0ebda4565ff421f322668ba2896.png

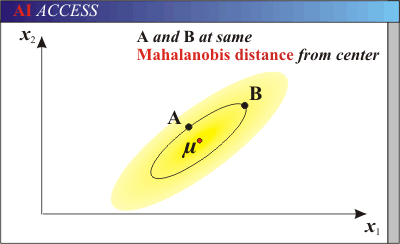
2ddd323d5c347f1a275368ae02b3acba.png

余弦距离

余弦距离，也称为余弦相似度，是用 $n$ 维空间中两点与原点连接线段之间夹角的余弦值作为衡量两个个体间差异的大小的度量。几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。

余弦距离越大，表示夹角越小，那么两点越相似。如果余弦距离为1（最大值），那么表示两者非常相似。注意这里只能说明两点非常相似，并不一定相同。

两个 $n$ 维样本点 $\mathbb{a}(x_{11}, x_{12}, \dots , x_{1n})$ 和 $\mathbb{b}(x_{21}, x_{22}, \dots, x_{2n})$ 的余弦距离公式:

\[\cos{(\theta)} = \frac{a \cdot b}{\left | a \right | \cdot \left | b \right | }\]

即

\[\cos{(\theta)} = \frac{\sum_{i-1}^n{x_{1i} \ x_{2i}}}{\sqrt{\sum_{k=1}^n{x_{1i}}^2} \ \sqrt{\sum_{k=1}^n{x_{2i}}^2}}\]

DeepSORT

DeepSort中使用了马氏距离来计算卡尔曼滤波状态和新获得的测量值（检测框）之间的距离。

\[d^{(1)}(i,j) = (d_j - y_i)^T S^{-1} (d_j - y_i)\]

$(y_i, S_i)$ 表示第 $i$ 个追踪分布在测量空间上的投影， $y_i$ 为均值， $S_i$ 为协方差矩阵， $i$ 表示追踪的序号， $j$ 表示检测框的序号

马氏距离通过测量卡尔曼滤波器的追踪位置均值（mean track location）之间的标准差与检测框来计算状态估计间的不确定性，即 $d^1(i,j)$ 为第 $i$ 个追踪分布和第 $j$ 个检测框之间的马氏距离（不确定度）。

论文中使用 $t = 9.4877$ 来作为马氏距离的阈值上限，超过则直接忽略。 $t$ 是由倒卡方分布计算出来的95%置信区间作为阈值。

0%