Hungarian Algorithm
Assignment Problem
The assignment prolem deals with assigning machines to tasks, workers to jobs, and so on.
The goal is to determine the optimum assignment that, for example, minimizes the total cost.
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法。
A special class of transportation problem is called assignment problems in which:
- ${supply}_i = {demand}_j = 1$
- 例如考虑每一个 worker 分配一个 job ,每一个 job 也都由一个 worker 来完成,当 workers 和 jobs 个数相等的话,要先考虑 workers 和 jobs 个数相等的情况。若 workers 和 jobs 不等的情况下,比如在多目标跟踪中, tracks 和 detects 可能是不相等的,需要做额外的处理。
- each decision variable is a binary decision varable (0,1)
- decision variable 也就是决策变量是个二进制的变量,在 (0,1) 中取值。
- all the constrains are in the form of equation (with “=” signs)
- 即有约束条件,是个等式。
Example
例如这里有4个起重机,每一个起重机分配一个任务。每个任务要求所需要的时间在表格中列出。
寻找最好的分配策略:即起重机工作总完成时间最少。
Find the best assignment of cranes to the jobs so the total cost required for completing the jobs is minimized:
| Job1 | Job2 | Job3 | Job4 | |
|---|---|---|---|---|
| crane1 | 4 ($x_{11}$) | 2 ($x_{12}$) | 5 ($x_{13}$) | 7 ($x_{14}$) |
| crane2 | 8 ($x_{21}$) | 3 ($x_{22}$) | 10 ($x_{23}$) | 8 ($x_{24}$) |
| crane3 | 12 ($x_{31}$) | 5 ($x_{32}$) | 4 ($x_{33}$) | 5 ($x_{34}$) |
| crane4 | 6 ($x_{41}$) | 3 ($x_{42}$) | 7 ($x_{43}$) | 14 ($x_{44}$) |
最优化的目标等于每个起重机完成的任务的时间乘以决策变量。
\[\begin{array}{lr} \begin{array}{rl} min \ Z \ = & 4 x_{11} + 2x_{12} + 5x_{13} + 7x_{14} + \\ & 8x_{21} + 3x_{22} + 10x_{23} + 8x_{24} + \\ & 12x_{31} + 5x_{32} + 4x_{33} + 5x_{34} + \\ & 6x_{41} + 3x_{42} + 7x_{43} + 14x_{44} \end{array} \end{array}\]其中,$x_{ij}$ 表示的是第 $i$ 个任务是否分配到第 $j$ 个起重机上,即决策变量。我们也可以列出对起重机和任务的约束条件。
\[\begin{array}{lr} cranes \ constraints \left\{ \begin{array}{lr} x_{11} + x_{12} + x_{13} + x_{14} = 1 & \\ x_{21} + x_{22} + x_{23} + x_{24} = 1 & \\ x_{31} + x_{32} + x_{33} + x_{34} = 1 & \\ x_{41} + x_{42} + x_{43} + x_{44} = 1 & \\ \end{array} \right. \\ \\ job \ constraints \left\{ \begin{array}{lr} x_{11} + x_{21} + x_{31} + x_{41} = 1 & \\ x_{12} + x_{22} + x_{32} + x_{42} = 1 & \\ x_{13} + x_{23} + x_{33} + x_{43} = 1 & \\ x_{14} + x_{24} + x_{34} + x_{44} = 1 & , \ \ x_{ij} = \begin{cases} 1 \ \ \ \ if \ i \ is \ allocated \ to \ j \\ 0 \ \ \ \ otherwise \end{cases} \\ \end{array} \right. \end{array}\]算法步骤
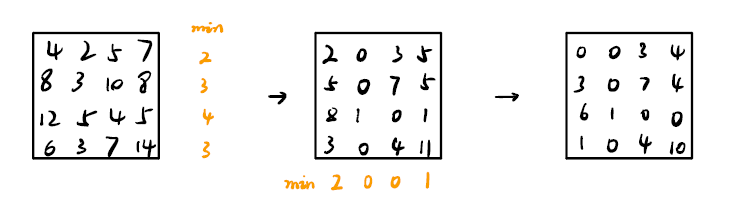
1. Row Reduction
Find the minimum of each row, and substract from each row the min value. 即找到每一行的最小值,并且每一行的值减去该最小值
2. Column Reduction
Find the minimum of each column, and substract from each column the min value. 找到每一列的最小值,并且每一列的值减去该最小值
过程如下:
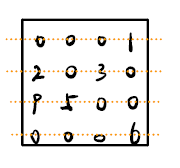
3. Cover all zeros with a minimum number of lines
意思就是说:找到最少的能够覆盖到矩阵中 $0$ 的线的个数,这些线可以是垂直的或水平的。
有可能会有多种情况出现,如图 orange lines 就是覆盖 $0$ 的线。
既然目前有两种情况,那就对这两种情况进行推导
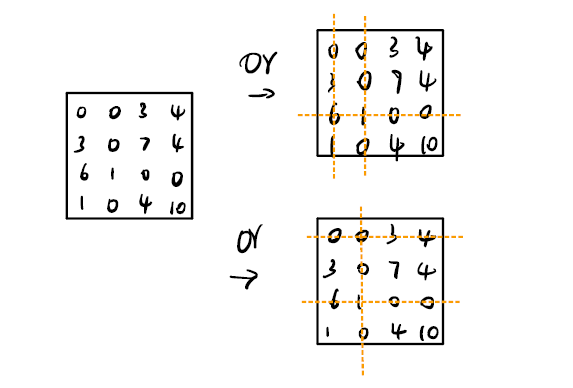
如果线的个数等于 $m$ (总行、列数)那可能找到了最优解了,否则到第四步继续运算。
当前线的个数为 $3 \ne m = 4$ ,因此我们继续看第四步。
4. Create additional zeros
即矩阵中 $0$ 的个数不够多,我们需要更进一步的操作让矩阵中有更多的 $0$ 。
- 先找到线未覆盖的区域中的最小值,然后这些未覆盖的区域中的值减去这个最小值
- 注意:线的交叉点的值要加上这个最小值
过程如图所示,红色的为未覆盖区域,蓝色的为交叉区域。
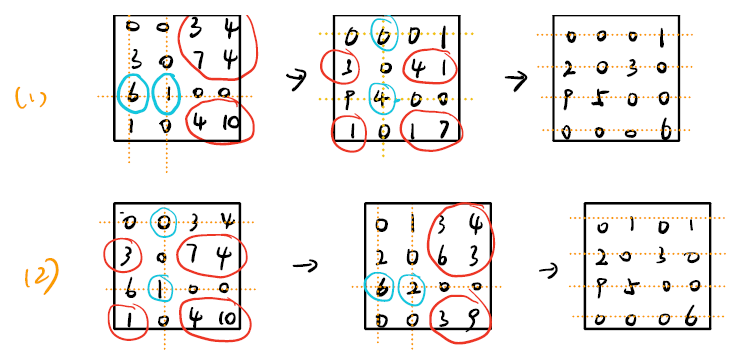
运算到最后我们发现,这两种情况最终都会得到一个相同的结果。
5. Making the final assignment
This is the final assignment.
最终我们得到最少线的数量为 $4 = m$ ,就得到了最优的表。
然后开始从拥有最少 $0$ 行或列中分配任务。过程如图所示:
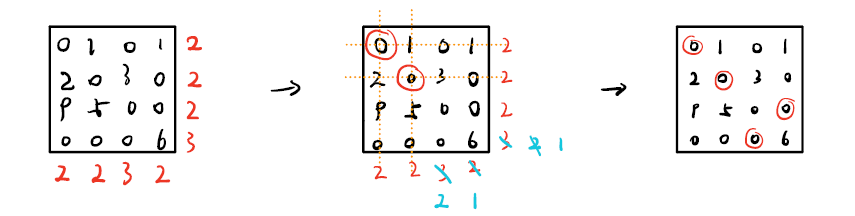
其过程是:首先把各行各列的 $0$ 的个数标注出来,然后从第一行第一列开始给每个起重机分配任务,每分配一个任务,那么后面再分配任务时,这一行或列中的任务会 -1 。
最终,我们得到了最优任务分配结果。我们之前也说过,决策变量为 1 时,代表该任务分配給对应列的起重机。
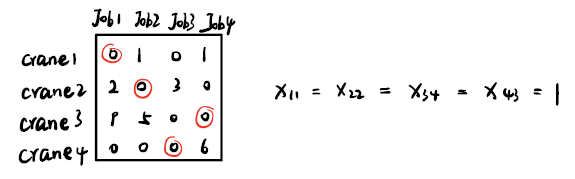
现在我们就可以计算最小的代价即最优解,这还需要回到原表中

即起重机工作总完成时间最少为19
DeepSORT中的作用
多目标跟踪在的视频中,不同时刻的同一个人,位置发生了变化,那么是如何关联上的?答案就是匈牙利算法和卡尔曼滤波。
- 匈牙利算法可以告诉我们当前帧的某个目标,是否与前一帧的某个目标相同。
- 卡尔曼滤波可以基于目标前一时刻的位置,来预测当前时刻的位置,并且可以比传感器(在目标跟踪中即目标检测器,比如Yolo等)更准确的估计目标的位置。
首先,由马氏距离 $d_1$ 以及余弦相识度 $d_2$ 得到的代价矩阵:
\[cost \ matrix = {\lambda} d_1 + (1 - {\lambda}) d_2\]而马氏距离与余弦相似度都是由 track 与 detection 计算来的。
也就是 track 与 detection 都是对应上面例子中的 crane 与 job 。
实际上匈牙利算法可以理解成“尽量多”的一种思路(尽可能的配对出多对(检测器+跟踪器))。
比如说 A 检测器可以和 a , c 跟踪器完成匹配(与a匹配置信度更高),但是 B 检测器只能和 a 跟踪器完成匹配。
那在算法中,就会让 A 与 c 完成匹配, B 与 a 完成匹配,而降低对于置信度的考虑。所以算法的根本目的并不是在于匹配的准不准,而是在于尽量多的匹配上,这也就是在 Deepsort 中作者添加级联匹配与马氏距离与余弦距离的根本目的。
也就是说,匈牙利算法是为了计算检测器(人)分配跟踪器(任务)的最优情况‘,用于后续的缓解ID switch