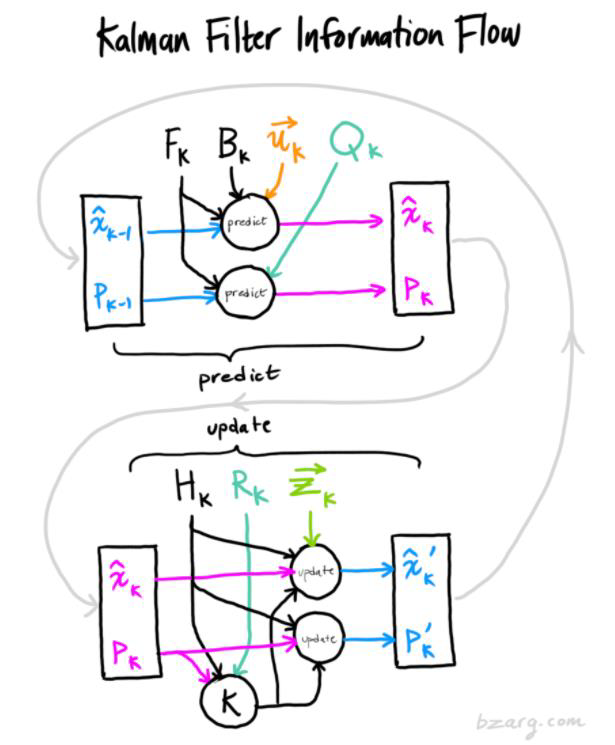
根据之前的卡尔曼滤波分析,知道了卡尔曼滤波分有 预测 和 更新 两步操作。本次则是分析:卡尔曼滤波在多目标跟踪中是如何应用的。
预测
首先是状态预测:新的最优估计是根据上一最优估计预测得到的
卡尔曼滤波假设两个变量(位置和速度)都是随机的且符合高斯分布。每个变量都有一个 均值 $\mu$ ,它是随机分布的中心;有一个方差 $\sigma^2$ ,它衡量组合不确定性
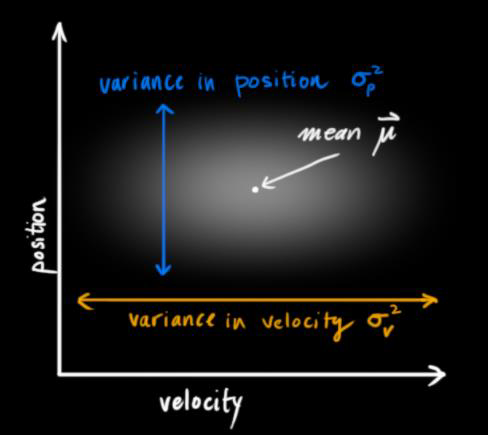
基于 track 在 $t-1$ 时刻的状态来预测其在 $t$ 时刻的状态
\[x' = Fx\]$x$ 为 track 在 $t-1$ 时刻的均值, $F$ 称为状态转移矩阵,该公式预测 $t$ 时刻的 $x’$
\[\begin{pmatrix} cx \\ cy \\ w \\ h \\ vx \\ vy \\ ww \\ vh \end{pmatrix} _t = \begin{pmatrix} 1 & 0 & 0 & 0 & dt & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & dt & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & dt & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & dt \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} cx \\ cy \\ w \\ h \\ vx \\ vy \\ ww \\ vh \end{pmatrix} \ \ \ \ \ \ (1)\]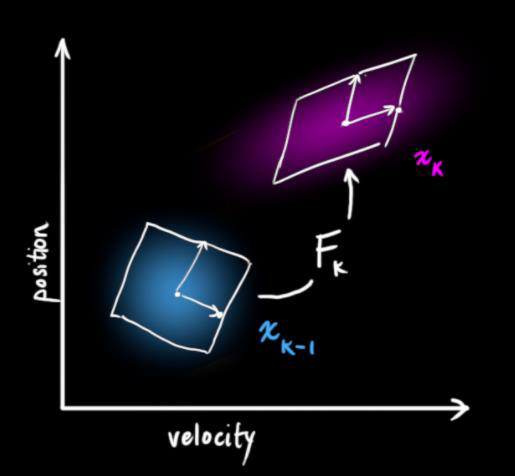
在 Deep SORT 中使用8个参数来进行运动状态的描述,其中 $(cx, cy)$ 是 bounding box 的中心坐标, $w$ 是长宽比, $h$ 是高度。其余四个变量表示对应的在图像坐标系中的速度信息。又因为是恒速运动所以状态矩阵中对角线数值为 1 。
协方差预测
根据图示,位置和速度是不相关,卡尔曼滤波就是为了从这种不相关的信息中尽可能找到的信息。
而为了捕获其相关性,则使用协方差矩阵表示位置和速度的互相关。图中白色区域表示两者的相关信息。
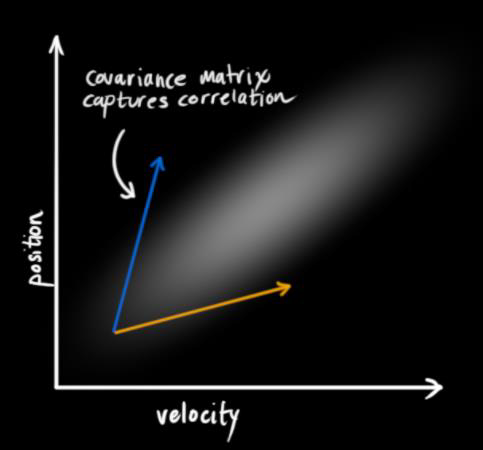
如果知道状态转移矩阵的话,我们可以根据状态转移矩阵求出下一时刻的协方差矩阵 $P’$ 。
\[P' = FPF^T + Q \ \ \ \ \ \ (2)\]新的不确定性由上一不确定性预测得到,并加上外部环境的干扰。
公式(2)预测 $t$ 时刻的协方差矩阵 $P’$ ,其中 $P$ 为 track 在 $t-1$ 时刻的协方差, $Q$ 为系统的 噪声矩阵 ,一般初始化为很小的值。
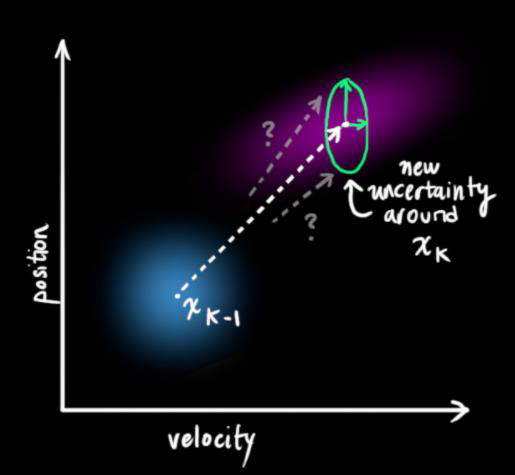
其中,协方差矩阵我们可以根据之前的文章:DeepSORT之马氏距离求得。
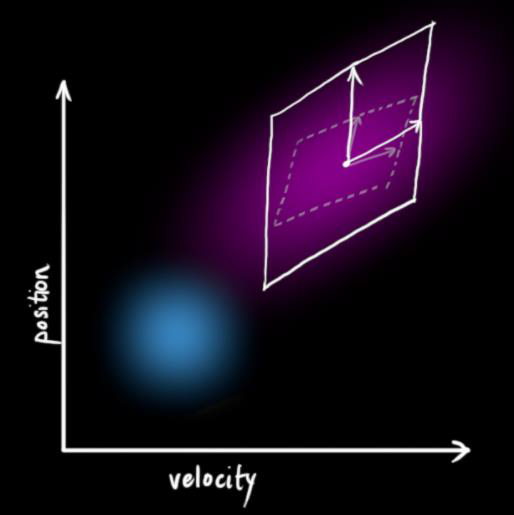
上图可以看到,由于噪声的影响,得到的数据拥有和原分布相同的均值,但协方差不同。
更新
基于 $t$ 时刻检测到的 detection,校正与其关联的 track 的状态,得到一个更精确的结果。
\[y = z - Hx' \ \ \ \ \ \ (3)\]在(3)中,$z$ 为 detection 的均值向量,不包含速度变化值,即 $z = [cx, cy, r, h]$ , $H$ 称为测量矩阵,它将 track 的均值向量 $x’$ 映射到测量空间,该公式计算 detection 和 track 的均值误差, $y$ 称为 innovation (新息)。
\[S = HP'H^T + R \ \ \ \ \ \ (4)\]在(4)中, $R$ 为检测器的噪声矩阵,它是一个 4x4 的对角矩阵,对角线上的值分别为中心点两个坐标以及宽高的噪声,以任意值初始化。该公式先将协方差矩阵 $P’$ 映射到测量空间,然后再加上噪声矩阵 $R$ 。
\[K = P'H^TS^{-1} \ \ \ \ \ \ (5)\]计算卡尔曼增益 $K$ ,卡尔曼增益用于估计误差的重要程度。
\[x = x' + Ky \ \ \ \ \ \ (6)\] \[P = (I - KH)P' \ \ \ \ \ \ (7)\](6)和(7)得到更新后的均值向量 $x$ 即当前时刻的状态估计和协方差矩阵 $P$ 。
以上步骤用图解表示:
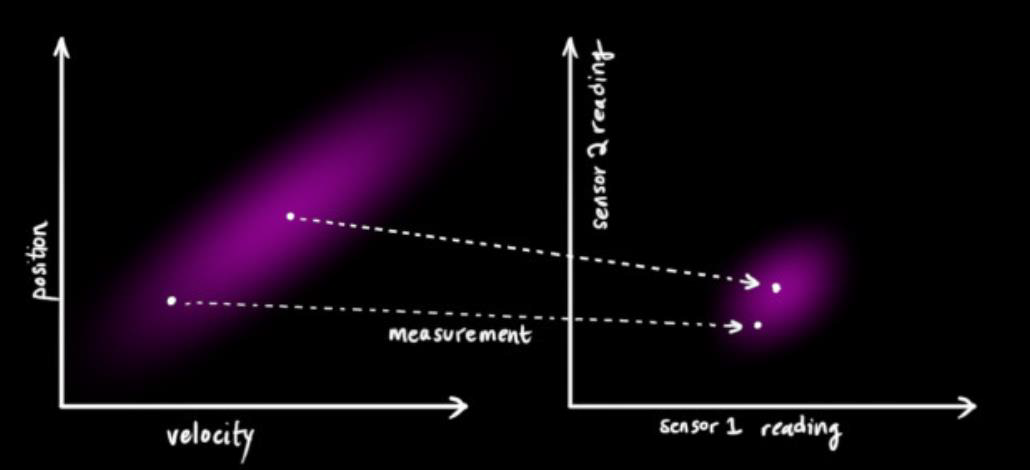
用测量值来修正估计值 $z_t = H_tx_t + v_t$
有了 measurement 以后需要映射到测量空间,测量空间是通过传感器 reading 等测量得到的。而这个映射就需要测量矩阵 $H_t$ ,公式为:
$\tilde{y}t=z_t-H_t\hat{x}{t \mid t-1}$
$S_t = H_tP_{t \mid t-1}H_t^T + R_t$
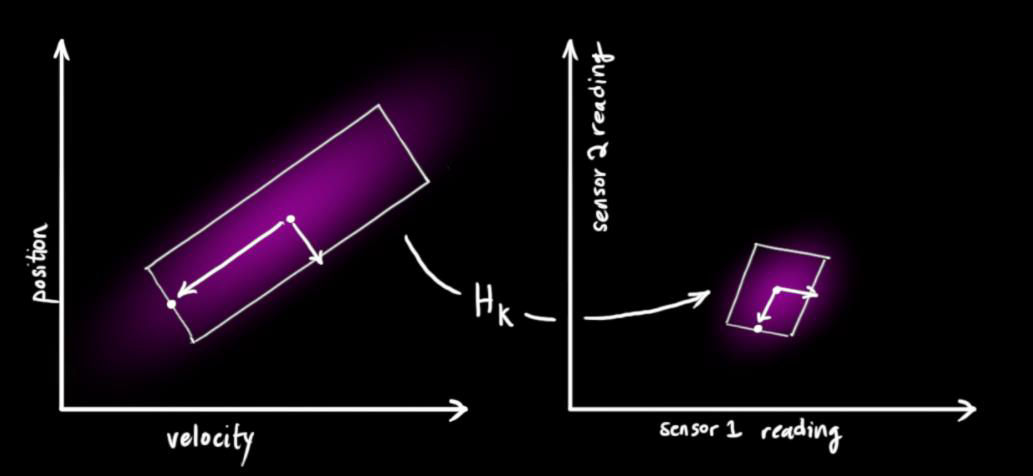
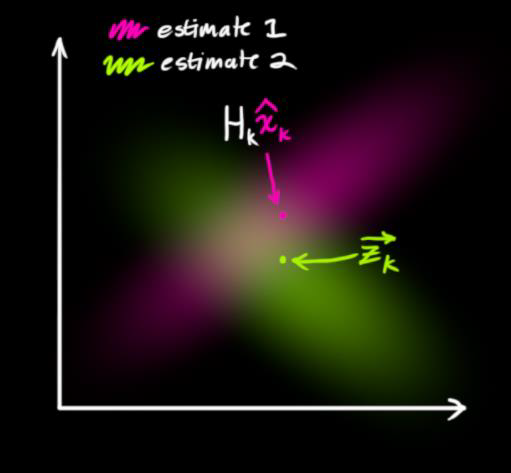
处理传感器噪声,在多目标中我理解为处理读取数据的噪声。这种不确定(噪声)的协方差设为 $R_k$ ,分布均值设为 $z_k$
那么就有了两部分高斯分布,一部分围绕预测的均值(粉红色),另一部分围绕读取的数据(绿色),然后在这之间找到最优解
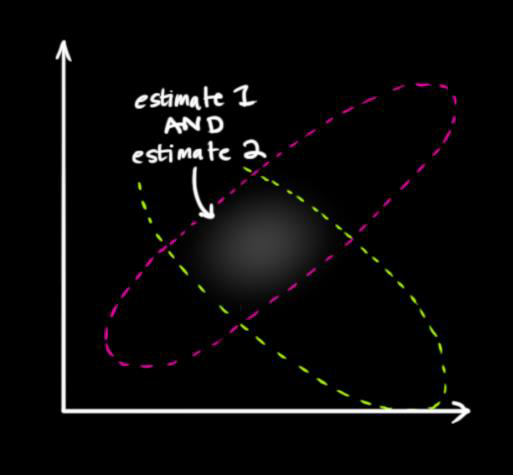
找最优解,就把两个具有不同均值和方差的高斯分布相乘,会得到一个新的具有独立值和方差的高斯分布
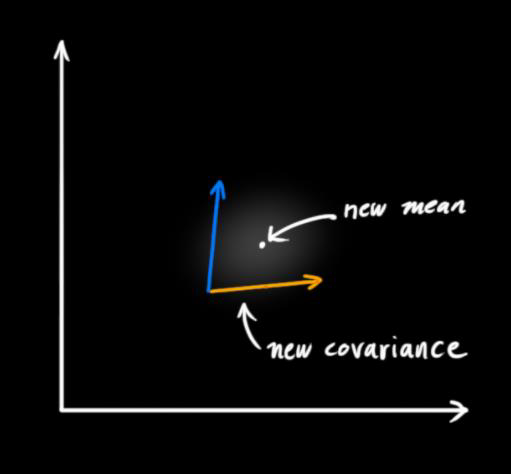
得到新的分布之后,就可以计算卡尔曼增益(Kalman Gain) $K$ :它表示我们应该集中注意预测值还是测量值的一个比例 $K_t = P_{t \mid t-1}H_t^TS_{-1}$
有了卡尔曼增益后,就可以更新状态 $x$ 和协方差矩阵 $P$
$\hat{x}{t \mid t}=\hat{x}{t \mid t-1}+K_t\tilde{y}_k$
$\hat{x}{t \mid t}=\hat{x}{t \mid t-1}+K_t(z_t-H\hat{x}_{t \mid t-1})$
$P_{t \mid t} = (I - K_tH_t)P_{t \mid t-1}$
接下来,把校正以后的值作为新的值再往前递推。再随着每帧的增加再进行卡尔曼滤波的一个过程。