LeetCode每日一题（四）：腐烂的橘子

发表于 | 分类于 | 阅读次数

暴力解决法、广度优先搜索( BFS )。不过中间求得时间次数需要一些巧妙的方法。

一、题目

在给定的网格中，每个单元格可以有以下三个值之一：

值 0 代表空单元格； 值 1 代表新鲜橘子； 值 2 代表腐烂的橘子。 每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1：

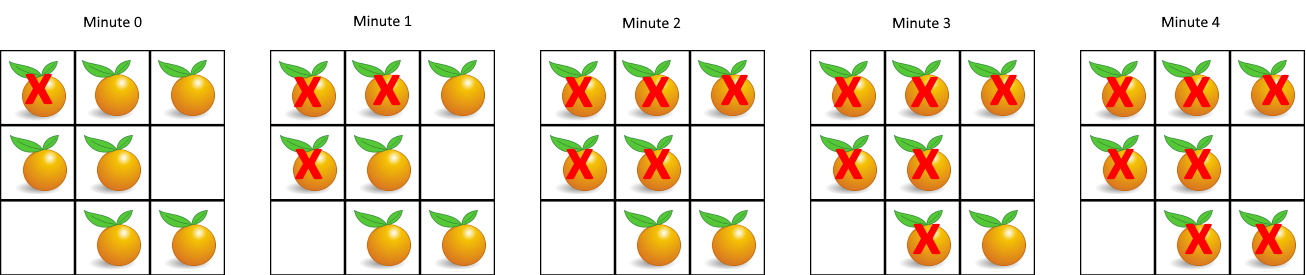
1
2
输入：[[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

1
2
3
输入：[[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

1
2
3
输入：[[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

二、思路

说实话，我一开始没有什么思路。看到评论说 BFS ,我才想起来广度优先搜索方法。

广度优先搜索

类似于二叉树的层次遍历算法，从起始顶点开始，依次访问邻接顶点，直到图中所有顶点都被访问过为止。并且借助队列，以记忆正在访问的顶点的下一层顶点。

其中有几个点需要 注意：

  1. 如何知道坏橘子的位置？
  2. 如何找相邻的橘子？
  3. 如何实现时间计数？

第一点好说，我们需要定义一个结构体作为队列元素的节点，节点中定义 x y 的坐标信息。只要将二维数组依次遍历，然后找出值等于 2 的橘子，同时将橘子的坐标存入节点信息中即可。

第二点：我们需要定义一个数组，存放方向值： int dy[] = {0,0,-1,1}; 和 int dx[] = {1,-1,0,0};。这样，我们可以找到上下左右相邻的橘子。

第三点：我们需要在节点信息中另外定义一个信息： cout 用来计数。当找到相邻的橘子时，计数+1，加一后的结果存放至相邻节点的信息中。注意：这里不止一个相邻节点。

三、代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#define NUM 100
#define DIRECTION_NUM 4

typedef struct {
    int x;
    int y;
    int counter;
}Node;

int orangesRotting(int** grid, int gridSize, int* gridColSize){
    if(grid == NULL || gridSize == 0 || gridColSize == NULL) {
        return -1;
    }
    Node queue[NUM];                            // 使用队列存放坏橘子
    Node cur;                                   // 找相邻橘子的中间变量
    int front = 0, rear  = 0;

    int x = 0, y = 0;                           // 相邻橘子的坐标
    int dy[] = {0,0,-1,1};                      // 从开始位置的上、下、左、右位置寻找相邻橘子
    int dx[] = {1,-1,0,0};                      

    int rows = gridSize;
    int cols = gridColSize[0];

    int timeCounter = 0;                        // 完全感染所需的时间

    int freshOrangeCounter = 0;
    int rottenOrangeCounter = 0;

    for(int i = 0;i < rows;i++) {
        for(int j = 0;j < cols;j++) {
            if(grid[i][j] == 1) {
                freshOrangeCounter++;
            }
            else if(grid[i][j] == 2) {
                rottenOrangeCounter++;
                queue[rear].x = i;              // 获取坏橘子的位置，存放至节点的信息中
                queue[rear].y = j;
                queue[rear++].counter = 0;
            }
        }
    }
    if(freshOrangeCounter == 0) {               // 新鲜橘子为0时，输出0
        return 0;
    }

    if(rottenOrangeCounter == 0) {              // 坏橘子为0时，输出-1
        return -1;
    }
    while(rear != front) {                      // 队列为空时，退出循环
        cur = queue[front++];                   // 坏橘子出队，赋给中间变量，开始找相邻的橘子

        if(freshOrangeCounter <= 0) {           // 新鲜橘子全部被感染，返回感染时间
            return timeCounter;
        }

        for(int i = 0; i < DIRECTION_NUM; i++) {
            x = cur.x + dx[i];
            y = cur.y + dy[i];
            if(x >= 0 && x < rows && y >= 0 && y < cols && grid[x][y] == 1) {
                freshOrangeCounter--;
                queue[rear].x = x;
                queue[rear].y = y;
                queue[rear++].counter = cur.counter + 1; // 相邻的坏橘子入队
                timeCounter = cur.counter + 1;
                grid[x][y] = 2;
            }
        }
    }
    return -1;
}

0%