LeetCode每日一题（七）：队列的最大值

发表于 | 分类于 | 阅读次数

分摊时间复杂度 ，敲黑板！要考的！

一、题目

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数 max_value 、 push_back 和 pop_front 的均摊时间复杂度都是 O(1) 。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1：

1
2
3
4
5
6
输入: 
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]

输出:
 [null,null,null,2,1,2]

示例 2：

1
2
3
4
5
6
输入: 
["MaxQueue","pop_front","max_value"]
[[],[],[]]

输出:
 [null,-1,-1]

限制：

  • 1 <= push_back,pop_front,max_value的总操作数 <= 10000
  • 1 <= value <= 10^5

二、思路

双端辅助队列

毕竟题目要求说了，时间复杂度为 O(1) 。所以除了用空间换时间，还真想不到什么好办法。

普通队列：就是用来正常存储数据的。

双端队列：是用来存储比较后的数据。也就是说，可以将最大值放置指定的位置，最后调用。那为什么选用双端队列？

根据双端队列的性质，队列的两端都可以执行入队和出队的操作。我们在将数据入队同时，还可以将数据与已入队的数据比较。

如果数据值小时，则直接入队。如果数据值大时，且队列不为空，则将除队头元素外的元素挨个出栈，直到队列为空时，重新入队。如图：

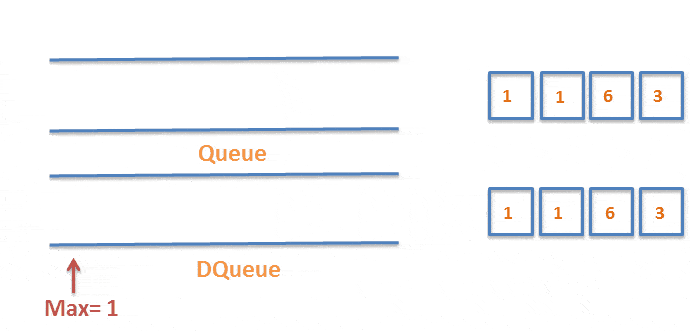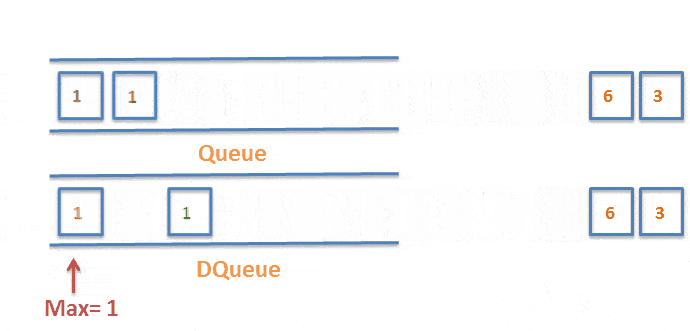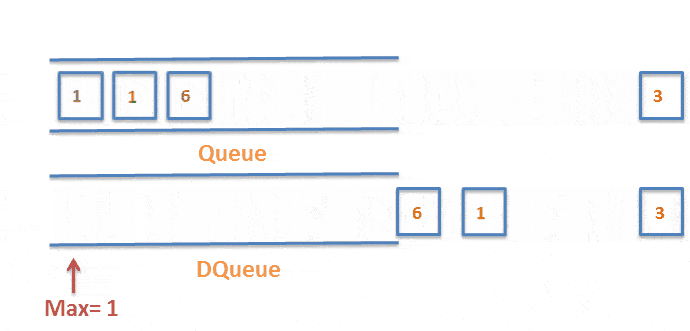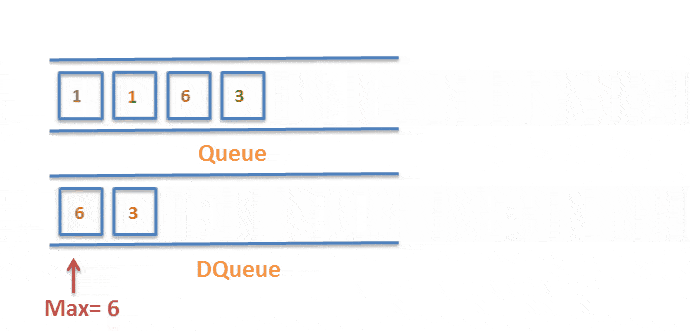
三、代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#define MAXSIZE 2048

typedef struct {
    int* data;
    int front, rear;
} Queue;

typedef struct {
    Queue* dataQue; // 循环队列，按正常顺序存储元素
    Queue* maxQue;  // 最大值存储在队头中的双端队列
} MaxQueue;

MaxQueue* maxQueueCreate() {
    MaxQueue *obj = (MaxQueue*)malloc(sizeof(MaxQueue));
    obj -> dataQue = (Queue*)malloc(sizeof(Queue));
    obj -> dataQue -> data = (int*)malloc(sizeof(int)*MAXSIZE);
    obj ->dataQue -> front = obj -> dataQue -> rear = 0;

    obj -> maxQue = (Queue*)malloc(sizeof(Queue));
    obj -> maxQue -> data = (int*)malloc(sizeof(int)*MAXSIZE);
    obj -> maxQue -> front = obj -> maxQue -> rear = 0;
    return obj;
}

void enQueue(Queue* q, int x) {
    q -> data[q -> rear++] = x;
    q -> rear %= MAXSIZE;
}

int deQueue(Queue* q) {
    int x = q -> data[q -> front++];
    q -> front %= MAXSIZE;
    return x;
}

bool isEmpty(Queue* q) {
    return q -> front == q -> rear;
}

// 获取对头元素：与队尾不同，队头指针一直指向空
int getFrontElem(Queue* q) {
    return q -> data[q -> front];
}

// 获取队尾元素
int getRearElem(Queue* q) {
    int rear = (q -> rear - 1 + MAXSIZE) % MAXSIZE;
    return q -> data[rear];
}

int maxQueueMax_value(MaxQueue* obj) {
    if (isEmpty(obj->dataQue)) {
        return -1;
    }
    return getFrontElem(obj -> maxQue);
}

void maxQueuePush_back(MaxQueue* obj, int value) {
    enQueue(obj -> dataQue, value);
    // 维护这个双端队列，保持队头指针指向最大值
    while(!isEmpty(obj -> maxQue) && getRearElem(obj -> maxQue) < value) {
        obj -> maxQue -> rear--;    // 当入队值大时，为指针重新指向队头的位置
    }
    enQueue(obj -> maxQue, value);
}

int maxQueuePop_front(MaxQueue* obj) {
    if (isEmpty(obj -> dataQue)) {
        return -1;
    }
    int x = deQueue(obj->dataQue);
    if (x == getFrontElem(obj->maxQue)) {
        deQueue(obj->maxQue);
    }
    return x;
}

void maxQueueFree(MaxQueue* obj) {
    free(obj -> dataQue -> data);
    free(obj -> dataQue);
    free(obj -> maxQue -> data);
    free(obj -> maxQue);
    free(obj);
}

0%