LeetCode：二叉树的直径

发表于 | 分类于 | 阅读次数

深度优先搜索( DFS )、二叉树递归遍历问题。

一、题目

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。

示例 :

给定二叉树

1
2
3
4
5
          1
         / \
        2   3
       / \     
      4   5

返回 3 , 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3] 。

注意：两结点之间的路径长度是以它们之间边的数目表示。

二、思路

深度优先搜索(DFS)

根据题目的说明，要找最大直径长度，但不一定要过根结点。如下图：

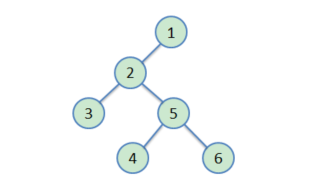
根据上图二叉树，我们可以找到它的最大直径长度：3 。其中有 [3, 2, 5, 4] 和 [3, 2, 5, 6] 两个路径。

为什么我们要使用深度优先搜索的方法？这里的深度优先搜索类似于 树的后序遍历（左右根） ，它是尽可能“深”地搜索一棵树，直到所有结点均被访问过。最后我们可以得出这棵树的高度与深度。

首先区别一下什么是 “树的高度与深度” 还有 “结点的深度与高度” 。

  • 结点的高度 ：是从叶子结点开始自底向上逐层累加的。
  • 结点的深度 ：是从结点开始开始自顶向下逐层累加的 （本题不计入该结点这一层）
  • 树的高度（深度）：就是树中结点的最大层数。

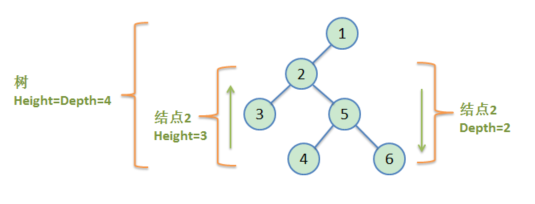
而本题中，我们对二叉树进行递归遍历，寻找某结点左右子树的最大深度。即每次都返回： max(L, R) + 1

左右子树的最大深度值进行计算：L + R + 1，可以得出该二叉树的最大直径。

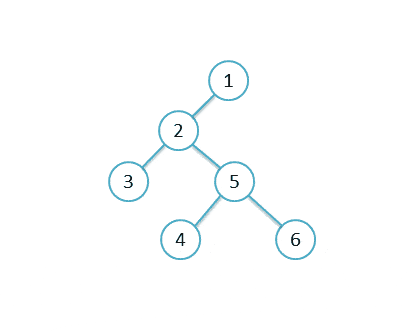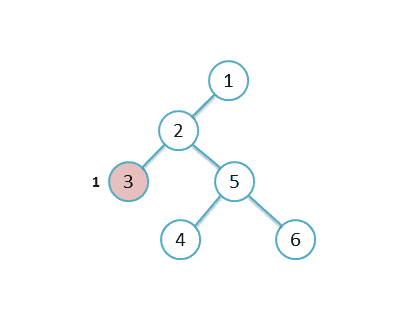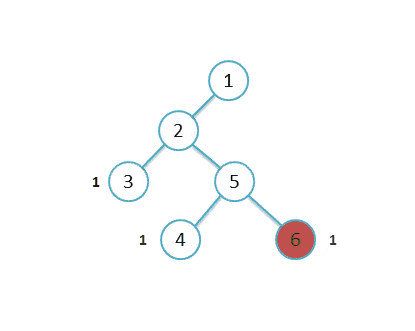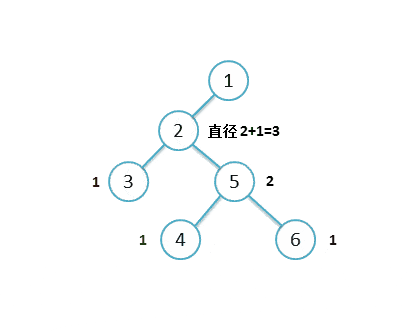
时间复杂度： O(n) 空间复杂度： O(height)

三、代码实现

C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define Max(a,b) a>b ? a+1 : b+1

int dfs(struct TreeNode* root, int *diam) {
    if(root == NULL) return 0;
    int leftDep = dfs(root -> left, diam);
    int rightDep = dfs(root -> right, diam);
    
    // *diam = leftDep + rightDep > *diam ? leftDep + rightDep : *diam;
    if(leftDep + rightDep > *diam)
        *diam = leftDep + rightDep;

    return Max(leftDep, rightDep);
}

int diameterOfBinaryTree(struct TreeNode* root){
    if(root != NULL) {
        int *diam = 0;
        dfs(root, &diam);
        return diam;
    }
    return 0;
}

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    int diam = 0;
public:
    int dfs(TreeNode* root) {
        if(root == NULL) return 0;
        int leftDep = dfs(root -> left);
        int rightDep = dfs(root -> right);
        
        diam = max(leftDep + rightDep, diam);

        return max(leftDep, rightDep) + 1;
    }

    int diameterOfBinaryTree(TreeNode* root) {
        if(root != NULL) {
            dfs(root);
            return diam;
        }
        return 0;
    }
};

0%